
Concevoir une expo, une visite guidée et des animations en mathématiques à partir du matériel créé par des enfants à l’école. Ma mission pour la Ville d’Eaubonne !
Depuis quelques années la ville d’Eaubonne, en Val-d’Oise, porte une attention particulière à la culture scientifique – en particulier mathématique – et offre à ses habitants des évènement culturels à thème. Ainsi, le festival Jeux Fêtes et Maths a lieu deux fois par an, grâce aussi au travail passionné de Denis Moreau, chargé de mission à la Direction de l’Action Culturelle. Cette année scolaire les services culturels ont proposé aux écoles de travailler sur les formes mathématiques. Les élèves, du CP à la seconde, ont visité l’exposition « Drôle de formes » en novembre 2019 lors du festival Jeux Fêtes et Maths et s’en sont inspirés pour travailler en classe par la suite. Le résultat de ce travail, un ensemble de jeux, panneaux, objets à exposer, vidéos, et autres belles choses, devait être mis en valeur et exposé, d’une façon qui puisse être également attrayante pour un public non scolaire.
Il m’arrive de travailler sur ce type de mission au moins une fois ou deux par an, et je trouve ces défis très stimulants. Les services culturels de la ville d’Eaubonne ont fait appel à moi pour cette mission dont les objectifs étaient :
- Trouver un fil conducteur reliant les travaux d’élèves
- Concevoir une exposition, un parcours de visité guidée et d’autres actions de médiation scientifique à partir de ce matériel pour le Festival Jeux Fêtes et Maths de février-mars 2020
Le résultat a été l’exposition collective « On va vous en faire voir de toutes les formes », accompagnée par des visites guidées et différents ateliers scientifiques pour les publics scolaires (de différents âges) et non scolaire. Le but de cette expo était de montrer que les mathématiques permettent de saisir le monde, avec des raisonnements logiques mais aussi en modélisant les éléments et les phénomènes naturels à partir de formes géométriques simples.

Voici une petite vidéo de la semaine de Festival. Après la vidéo vous trouverez un aperçu de l’expo et un panorama des activités de médiation, j’espère que ça puisse inspirer qui souhaite mettre en place des activités de ce type.
Tampons tangram

On commence par deux activités créées par les plus petits, où art et sciences se mélangent. En effet comme pour l’art, il faut de la créativité pour chercher d’expliquer le monde avec les maths, on peut même dire que les mathématiciens sont des créatifs ! Dans cette première section de l’expo on voit des œuvres réalisées avec des tampons encreurs à partir des formes du Tangram. Le Tangram est un jeux formé par un carré décomposé en sept pièces élémentaires (5 triangles isocèles rectangles, 1 carré et 1 parallélogramme) qui peuvent être recomposées en de très nombreuses façon. Le jeu du Tangram a été le point de départ pour comprendre qu’on peut reconstituer, de façon approximative, une figure connue à partir de formes élémentaires. Les enfants ont modélisé des personnages ou des objets comme cette fusée, mais aussi des formes abstraites.
Les enfants se sont aussi inspirés e cette vidéo
BD hexagonales

Lors de cette deuxième activité, les enfants ont découvert le pavage d’une surface plane par une forme hexagonale, à travers la création d’une BD sur des cases à forme d’hexagone. Ils ont ainsi découvert une manière originale de parcourir le plan. On peut lire différentes histoires en suivant plusieurs directions. L’idée originale est du dessinateur Etienne Lécroart qui a créé de nombreuses bandes dessinées à partir de contraintes mathématiques et qui a illustré un livre du célèbre mathématicien Cédric Villani. Pour reprendre le thème du pavage rendons nous dans une autre section de l’expo.
Les mosaïques arabes
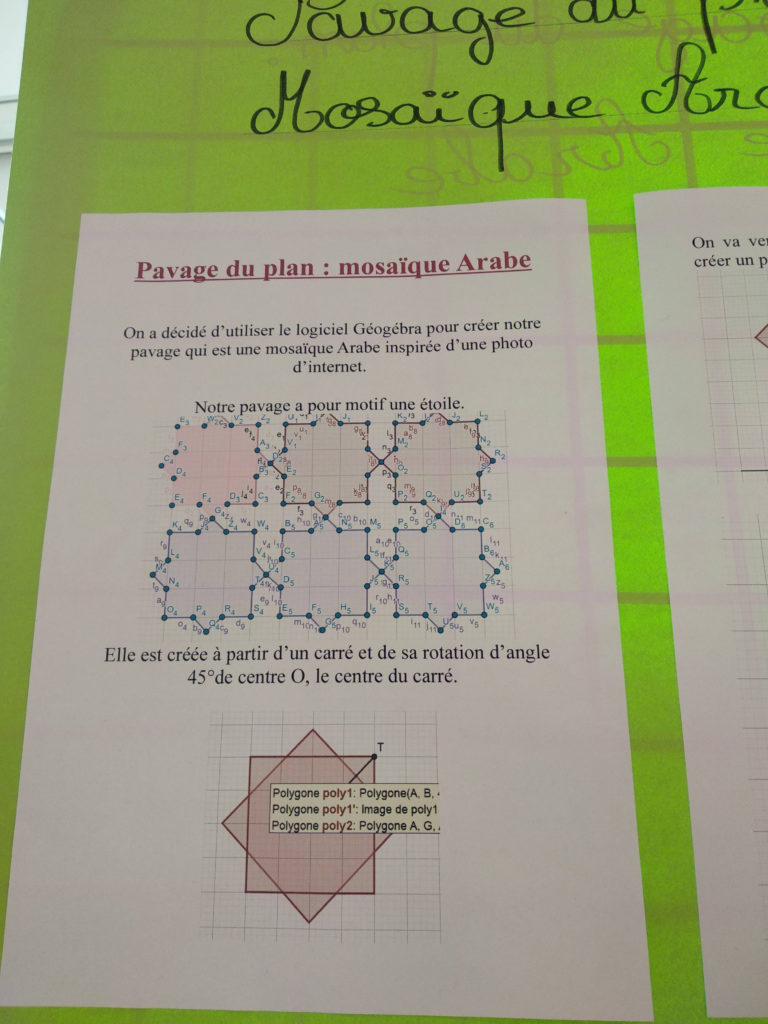
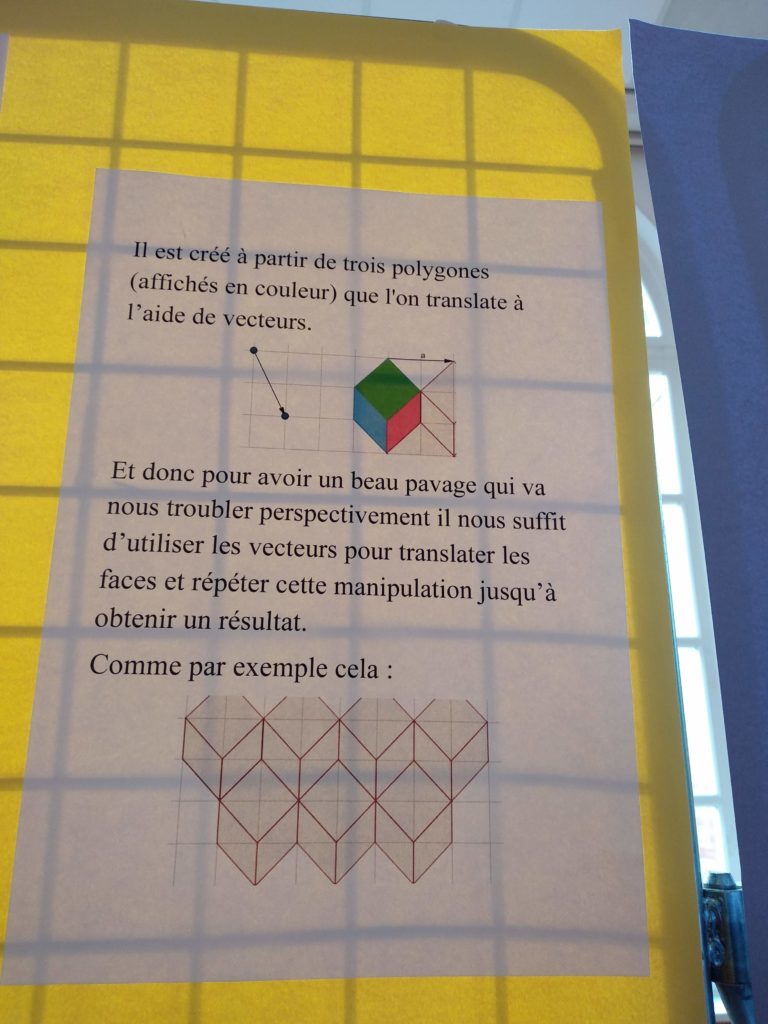
Ici les élèves de seconde ont étudié les mosaïques arabes et d’autres pavages décoratifs du sol et du mur. Paver une surface veut dire la remplir avec un motif qui se répète sans laisser d’espaces vides. Il y a plusieurs façons d’obtenir un pavage à partir d’une figure donnée, les lycéens ont utilisé le logiciel Geogebra pour les construire. Par exemple ils ont utilisé une rotation de 45 degrés pour créer une étoile à partir d’un carré, et une translation (une espèce de glissement sans changement de forme) de trois polygones pour obtenir un effet tridimensionnel. Dans ces pavages aussi les mathématiques se confondent avec l’art. Leur aspect décoratif et le plaisir pour les yeux étaient connus depuis longtemps et ne cessent pas de nous plaire ! Mais les mathématiques peuvent aussi nous étonner en nous montrant une beauté un peu plus cachée.
Dessiner des tables de multiplication


Les tables de multiplications sont un exercice parfois un peu ennuyeux, mais si on y travaille de façon graphique on peut obtenir des résultats assez étonnants ! Normalement, quand nous imaginons la représentation graphique des nombres, nous les imaginons placés sur une ligne qui tend vers l’infini : 1, 2, 3, 4, 5, 6… Ici les nombres ont été placés sur un cercle, qui est fini. C’est un peu comme les heures sur le cadre d’un horloge. C’est ce qu’on appelle l’arithmétique modulaire. Ces tables sont construites en représentant, avec des lignes, les résultats des calculs des multiplications sur un cercle. Par exemple pour la table du 2 on relie chaque nombre avec son résultat quand il est multiplié par 2. Au bout d’un certain nombre de multiplications on verra apparaître des jolies figures, par exemple des rosaces ou des cardioïdes, des figures qui rappellent la forme du cœur. Si on fait des multiplications plus difficiles on va découvrir des figures très complexes mais toujours symétriques et de grande beauté.
Jouer avec les polyèdres

Si dans le cas des multiplications on part des nombres et des opérations et on arrive à une représentation graphique, dans le cas des polyèdres on peut faire le contraire. A travers les jeux sur les polyèdres créés par des élèves de CM2, les mathématiques ne se font pas avec des nombres, mais avec des formes en 3 dimensions. On les manipule et on découvre des propriétés, des théorèmes, qu’on peut ensuite chercher à démontrer. Ces polyèdres peuvent modéliser des objets de la vie de tous les jours, par exemple une toupie, une balançoire ou l’icosaèdre qui peut représenter le ballon de football. En parlant de ballon de football, on peut aussi revenir à parler de pavage mais cette fois d’une surface sphérique. Par exemple les ingénieurs de Adidas ont redécouvert un théorème mathématique en cherchant une solution pour paver le ballon Brazuka. Comme quoi les mathématiques ne sont pas du tout éloignées de la vie de tous les jours comme le pensent certains ! Dans les sections suivantes on découvre bien d’autres exemples.
Des fractales partout !

Un peu comme on a vu avec l’exemple du Tangram, les mathématiciens utilisent parfois des formes géométriques ou des concepts mathématiques pour comprendre les formes plus complexes de la nature. Si on observe par exemple une feuille de fougère, le chou romanesco ou les branches d’un arbre, on se rend compte qu’il y a des motifs répétés d’une régularité surprenante. La nature en effet trouve la solution optimale d’un point de vue mathématique. Les objets mathématiques qui ressemblent le plus à la fougère et à l’arbre son appelés fractales.
Les fractales sont des objets mathématiques qui sont semblables à eux-mêmes à n’importe quelle échelle. Ça veut dire que si on zoome on voit toujours la même structure qui se répète. On dit qu’ils sont autosimilaires. Les fractales ont été découverts à partir du début du XXème siècle mais ils ont été popularisés à la fin des années 1960 par Benoît Mandelbrot. Ici les élèves ont présenté les plus connus : le flocon de Koch, le triangle de Sierpinski et l’éponge de Menger.
Flocon de Koch
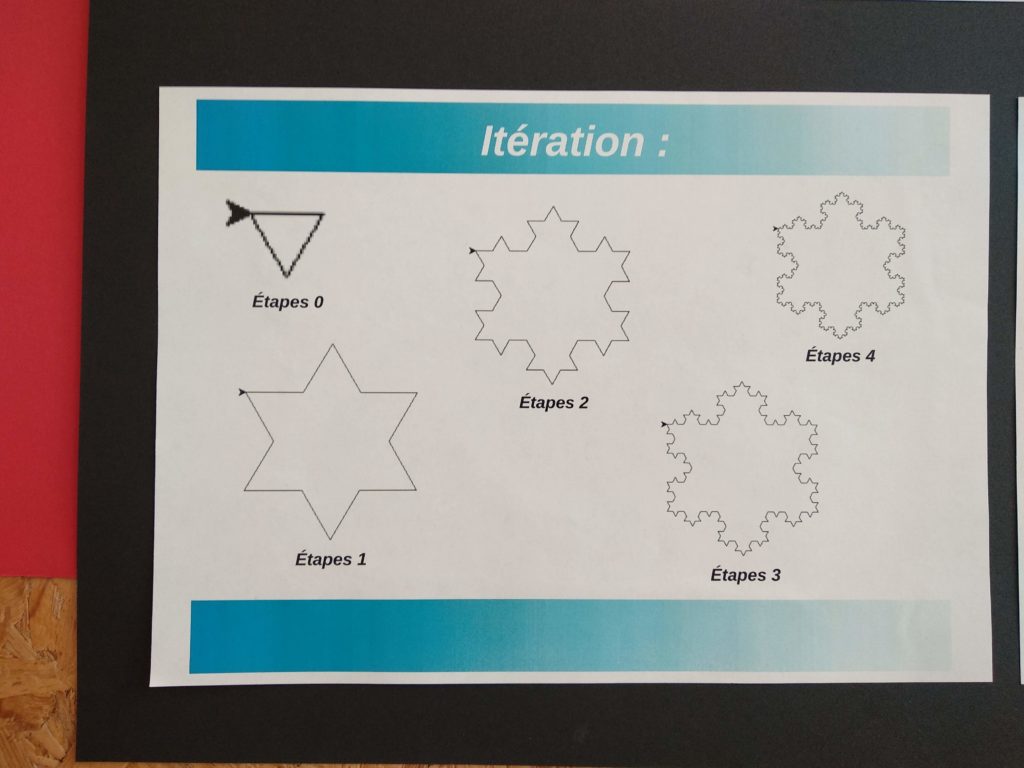
Le Flocon de Koch a été une des premières fractales découverts. Pour le construire on enlève le tiers central de chaque côté d’un triangle équilatéral et on y met deux segments de la même longueur, pour former un autre triangle dans le triangle. On obtient ainsi d’abord une étoile et puis des figures de plus en plus complexes qui ressemblent à des flocons de neige et on les appelle courbes de Koch (et leur longueur est infinie). La technique que nous avons utilisé s’appelle itération, ça veut dire répétition.
Le triangle de Sierpinski

Même le triangle de Sierpinski est construit avec des itérations. D’abord un prend un triangle équilatéral « plein » et puis on réunit les milieux des côtés entre eux en obtenant un triangle interne qu’on enlève. Comme ça nous avons obtenu 4 triangles identiques mais celui central est vide. La longueur de ces triangles est la moitié du triangle de départ, alors que l’aire est un quart. On peut répéter cette opération à l’infini. Comme on l’a vu, la longueur et l’aire n’augmentent pas de la même façon et ne respectent pas les caractéristiques des figures géométriques « normales ». Plus le périmètre augmente plus l’aire diminue et viceversa, au contraire des figures normales. Son périmètre tend vers infini et son aire vers zéro. Pour mieux comprendre que le triangle de Sierpinski est créé à partir d’une série d’itérations (ou répétitions) les élèves ont fait ce pliage fractal.
Eponge de Menger

L’éponge de Menger est un solide fractal qui rappelle une éponge parce qu’il est vide à l’intérieur. Pour le construire on prend un cube, puis on le divise 20 cubes qui ont le côtés d’un tiers par rapport au cube initial, et puis on positionne ces 20 petits cubes à former un cube qui ressemble à celui initial mais vide à l’intérieur. On peut continuer comme ça à l’infini et le cube sera de plus en plus vide. A chaque itération on multiplie le nombre de cubes par 20.
Avec le triangle de Sierpinski ou l’éponge de Menger on voit bien qu’à partir d’une figure abstraite et d’un théorème théorique nous pouvons faire des similitudes avec des choses existantes. Par exemple la structure des poumons. Les alvéoles pulmonaires sont extrêmement ramifiés, comme une structure fractale, pour occuper le maximum de surface (pour les échanges d’air de de CO2) dans un volume fixe (la cage thoracique). De la même manière se comportent les villosités intestinales : l’abdomen a un volume limité et les villosités augmentent la surface. C’est la même chose qui arrive à l’éponge de Menger : son volume extérieur est fixe, mais au fur et à mesure qu’on le créé, il aura de plus en plus de surfaces à l’intérieur.
Ensembles de Julia
Durant les cours en informatique les élèves de première et seconde ont utilisé le langage de programmation Phyton pour créer des fractales particulières appelés l’ensemble de Mandelbrot et les ensembles de Julia, du nom du mathématicien Gaston Julia. Comme pour les tables de multiplications, on s’aperçoit que des formes étranges et fascinantes peuvent apparaître quand on fait des opérations très mathématiques.

excellent travail c’est vraiment magnifique merci d’voir partager
Merci beaucoup à vous !